All LeetCode Blind-75 Solutions Using Python
Blind-75 is a curated list of 75 LeetCode problems compiled by Yangshun Tay. The list can be accessed on this link.
I have provided Python solutions for all the problems on the list, along with their respective time and space complexities. These solutions can also be found on my GitHub repository titled "leetrank".
Two Sum
Given an array of integers nums and an integer target, return indices of the two numbers such that they add up to target.
1def two_sum_hash(arr, target):
2 hash_table = {} # key: num, value: index
3
4 for idx, num in enumerate(arr):
5 # Compute the complement of the current element
6 # (i.e. the number we need to find in order to sum up to the target)
7 complement = target - num
8 # If the complement exists in the dictionary,
9 # then we have found the two elements that sum up to the target
10 if complement in hash_table:
11 return [hash_table[complement], idx]
12 # Otherwise, add the current element to the dictionary
13 hash_table[num] = idx
14
15 # If we reach this point, it means we did not find the two elements that sum up to the target
16 return []
Time complexity of the above code is O(n), where n is the length of the input array arr. This is because the for loop iterates over all elements in the array, and the dictionary lookups and updates are O(1) operations.
Space complexity of the above code is also O(n), because the dictionary uses O(n) space to store the indexes of all the elements in the array. This means that the space complexity is linear in the size of the input.
Best Time to Buy and Sell Stock
You are given an array prices where prices[i] is the price of a given stock on the ith day.
You want to maximize your profit by choosing a single day to buy one stock and choosing a different day in the future to sell that stock.
Return the maximum profit you can achieve from this transaction. If you cannot achieve any profit, return 0.
1Input: prices = [7,1,5,3,6,4]
2Output: 5
3Explanation: Buy on day 2 (price = 1) and sell on day 5 (price = 6), profit = 6-1 = 5.
4Note that buying on day 2 and selling on day 1 is not allowed because you must buy before you sell.
1class Solution:
2 def maxProfit(self, prices):
3 # lru_cache decorator that applies memoization to the `recursion` function
4 # so that it will only compute values for a given time and stock state once,
5 @lru_cache(None)
6
7 def recursion(time, stock, count):
8
9 # If the number of transactions is greater than 1, we can't make any more
10 # transactions, so we return 0.
11 if k > 1: return 0
12
13 # If the time is greater than or equal to the length of the prices list,
14 # then we have reached the end of the prices, so we return 0.
15 if time >= len(prices): return 0
16
17 # If we don't have any stock, we can buy one at the current time and price.
18 buy = -prices[time] + recursion(time + 1, stock + 1, count) if stock == 0 else float("-inf")
19
20 # If we have stock, we can sell it at the current time and price.
21 sell = prices[time] + recursion(time + 1, stock + 1, count+1) if stock == 1 else float("-inf")
22
23 # If we neither buy nor sell, we hold our current stock.
24 hold = 0 + recursion(time + 1, stock, count)
25
26 # Return the maximum of the three possible actions: buy, sell, or hold.
27 return max(buy, sell, hold)
28
29 # Set the maximum number of transactions to 1.
30 k = 1
31
32 return recursion(0, 0, 0)
The time complexity of the code is exponential in the length of the prices list. This is because the recursion function is called repeatedly for each possible combination of time, stock state, and count of transactions, and the number of possible combinations grows exponentially with the length of the prices list.
The space complexity of the code is also exponential in the length of the prices list. This is because the recursion function calls itself repeatedly, and each recursive call adds a new entry to the call stack. Since the number of recursive calls grows exponentially with the length of the prices list, the size of the call stack also grows exponentially, leading to an exponential space complexity.
The lru_cache decorator helps to improve the performance of the code by avoiding redundant calculations and storing the results in a cache, but it does not affect the time and space complexity of the code.
Contains Duplicate
Given an integer array nums, return true if any value appears at least twice in the array, and return false if every element is distinct.
1Input: nums = [1,2,3,1]
2Output: true
1class Solution:
2 def containsDuplicate(self, nums: List[int]) -> bool:
3 # Create a set to store the numbers we have seen.
4 seen = set()
5
6 # Iterate over the numbers in the input list.
7 for num in nums:
8 # If we have seen the current number before, return True.
9 if num in seen:
10 return True
11
12 # Add the current number to the set of seen numbers.
13 seen.add(num)
14
15 # If we reach here, it means we haven't seen any duplicates, so return False.
16 return False
The time complexity of this code is linear in the length of the nums list. This is because we need to iterate over the list once and perform a constant-time set membership check on each element. The space complexity is also linear in the length of the nums list, because we need to store each element of the list in the seen set. So, O(n).
Product of Array Except Self
Given an integer array nums, return an array answer such that answer[i] is equal to the product of all the elements of nums except nums[i].
You must write an algorithm that runs in O(n) time and without using the division operation.
1Input: nums = [1,2,3,4]
2Output: [24,12,8,6]
1class Solution:
2 def productExceptSelf(self, nums: List[int]) -> List[int]:
3
4 # Create an array to store the product of all the numbers on the left of the current number.
5 left = []
6
7 # Initialize the product to 1.
8 product = 1
9
10 # Loop through the numbers in the input array.
11 for num in nums:
12 # Append the current product to the left array.
13 left.append(product)
14 # Update the product with the current number.
15 product *= num
16
17 # Create an array to store the product of all the numbers on the right of the current number.
18 right = []
19 # Initialize the product to 1.
20 product = 1
21
22 # Loop through the numbers in the input array in reverse order.
23 for num in reversed(nums):
24 # Append the current product to the right array.
25 right.append(product)
26 # Update the product with the current number.
27 product *= num
28
29 # Reverse the right array so it is in the correct order.
30 right = list(reversed(right))
31
32 # Create an array to store the result.
33 result = []
34
35 # Loop through the numbers in the input array.
36 for i in range(len(nums)):
37 # Append the product of the current number's corresponding left and right numbers to the result.
38 result.append(left[i] * right[i])
39
40 # Return the result array.
41 return result
The time complexity of the above code is O(n). It loops through the input array once to compute the left array and once to compute the right array, and then loops through the input array again to compute the result array. Since the loop runs in linear time with respect to the size of the input array, the overall time complexity is O(n).
The space complexity of the above code is O(n). It creates three arrays of the same size as the input array: the left array, the right array, and the result array. Since the size of these arrays is directly proportional to the size of the input array, the space complexity is O(n).
Maximum Subarray
Given an integer array nums, find the subarray which has the largest sum and return its sum.
1Input: nums = [-2,1,-3,4,-1,2,1,-5,4]
2Output: 6
3Explanation: [4,-1,2,1] has the largest sum = 6.
1class Solution:
2 def maxSubArray(self, nums: List[int]) -> int:
3 # Initialize the maximum sum with the first number in the input array.
4 max_sum = current_sum = nums[0]
5
6 # Loop through the numbers in the input array starting from the second number.
7 for num in nums[1:]:
8 # Update the current sum by taking the maximum of the current number
9 # and the current number plus the current sum.
10 current_sum = max(num, num + current_sum)
11 # Update the maximum sum with the maximum of the current sum and the maximum sum.
12 max_sum = max(max_sum, current_sum)
13
14 # Return the maximum sum.
15 return max_sum
The time complexity of the above code is O(n), where n is the number of elements in the input array nums. This is because the for loop iterates over all elements in the input array.
The space complexity of the above code is O(1), because it only uses a constant amount of memory to store a few variables, regardless of the size of the input.
Maximum Product Subarray
Given an integer array nums, find a subarray that has the largest product, and return the product.
1Input: nums = [2,3,-2,4]
2Output: 6
3Explanation: [2,3] has the largest product 6.
1class Solution:
2 def maxProduct(self, nums: List[int]) -> int:
3 max_product = min_product = nums[0]
4
5 # Initialize the maximum product found so far to the first element
6 max_so_far = nums[0]
7
8 # Iterate through the array, starting from the second element
9 for i in range(1, len(nums)):
10 # Find the maximum and minimum product of the current element and the current product
11 max_product, min_product = max(nums[i], max_product * nums[i], min_product * nums[i]), min(nums[i], max_product * nums[i], min_product * nums[i])
12 # Update the maximum product found so far
13 max_so_far = max(max_so_far, max_product)
14
15 return max_so_far
The time complexity of the above code is O(n), where n is the number of elements in the input array nums. This is because the for loop iterates over all elements in the input array.
The space complexity of the above code is O(1), because it only uses a constant amount of memory to store a few variables, regardless of the size of the input.
Find Minimum in Rotated Sorted Array
Suppose an array of length n sorted in ascending order is rotated between 1 and n times. For example, the array nums = [0,1,2,4,5,6,7] might become:
[4,5,6,7,0,1,2]if it was rotated4times.[0,1,2,4,5,6,7]if it was rotated7times.
Notice that rotating an array [a[0], a[1], a[2], ..., a[n-1]] 1 time results in the array [a[n-1], a[0], a[1], a[2], ..., a[n-2]].
Given the sorted rotated array nums of unique elements, return the minimum element of this array.
You must write an algorithm that runs in O(log n) time.
1Input: nums = [3,4,5,1,2]
2Output: 1
3Explanation: The original array was [1,2,3,4,5] rotated 3 times.
1class Solution:
2 def findMin(self, nums: List[int]) -> int:
3 # Set the left and right indices for the binary search
4 left, right = 0, len(nums) - 1
5
6 # Perform binary search to find the minimum value
7 while left < right:
8 # Calculate the midpoint of the current search range
9 mid = (left + right) // 2
10
11 # If the midpoint value is greater than the rightmost value,
12 # the minimum value must be in the right half of the array
13 if nums[mid] > nums[right]:
14 left = mid + 1
15 else:
16 # If the midpoint value is not greater than the rightmost value,
17 # the minimum value must be in the left half of the array
18 right = mid
19
20 # Return the minimum value, which will be at the left index
21 return nums[left]
The time complexity of the above code is O(log n), where n is the length of the array. This is because the binary search reduces the search range by half in each iteration, so the number of iterations required is determined by the number of times n can be divided by 2 before reaching 1. The space complexity is O(1), since the code only uses a constant number of variables regardless of the size of the input array.
Search in Rotated Sorted Array
There is an integer array nums sorted in ascending order (with distinct values). Given the array nums after the possible rotation and an integer target, return the index of target if it is in nums, or -1 if it is not in nums.
You must write an algorithm with O(log n) runtime complexity.
1Input: nums = [4,5,6,7,0,1,2], target = 0
2Output: 4
1class Solution:
2 def search(self, nums: List[int], target: int) -> int:
3
4 # Initialize left and right pointers
5 left = 0
6 right = len(nums) - 1
7
8 # Keep looping until left pointer is less than or equal to right pointer
9 while left <= right:
10 # Calculate middle index
11 mid = (left + right) // 2
12
13 # If target is at middle index, return middle index
14 if target == nums[mid]:
15 return mid
16
17 # If left side is sorted
18 if nums[left] <= nums[mid]:
19 # If target is in left side, update right pointer to middle index - 1
20 if nums[left] <= target <= nums[mid]:
21 right = mid - 1
22 # Else, update left pointer to middle index + 1
23 else:
24 left = mid + 1
25 # Else, right side is sorted
26 else:
27 # If target is in right side, update left pointer to middle index + 1
28 if nums[mid] <= target <= nums[right]:
29 left = mid + 1
30 # Else, update right pointer to middle index - 1
31 else:
32 right = mid - 1
33
34 # Target not found, return -1
35 return -1
The time complexity of the above code is O(log n) because in each iteration, the search space is halved. This is because the code uses binary search to find the target element in the given list.
The space complexity of the above code is O(1), because the code does not use any additional memory space proportional to the size of the input. The only variables used are the left and right pointers, which remain constant regardless of the size of the input list.
3 Sum
Given an integer array nums, return all the triplets [nums[i], nums[j], nums[k]] such that i != j, i != k, and j != k, and nums[i] + nums[j] + nums[k] == 0.
Notice that the solution set must not contain duplicate triplets.
1Input: nums = [-1,0,1,2,-1,-4]
2Output: [[-1,-1,2],[-1,0,1]]
3Explanation:
4nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0.
5nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0.
6nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0.
7The distinct triplets are [-1,0,1] and [-1,-1,2].
8Notice that the order of the output and the order of the triplets does not matter.
1class Solution:
2 def threeSum(self, nums: List[int]) -> List[List[int]]:
3 # Sort the input list
4 nums.sort()
5
6 # Initialize empty list to store triplets
7 triplets = []
8
9 # If the length of the input list is less than 3, return empty list
10 if len(nums) < 3:
11 return []
12
13 # Loop through all elements in the list except the last two
14 for i in range(len(nums) - 2):
15 # Initialize left pointer to the element after current element
16 left = i+1
17 # Initialize right pointer to the last element in the list
18 right = len(nums) -1
19
20 # Keep looping until left pointer is less than right pointer
21 while left < right:
22 # Calculate the sum of the current element, left element, and right element
23 sums3 = nums[i] + nums[left] + nums[right]
24 # If the sum is 0, append the current triplet to the triplets list and update the left and right pointers
25 if sums3 == 0:
26 triplets.append((nums[i], nums[left], nums[right]))
27 left += 1
28 right -= 1
29 # If the sum is less than 0, update the left pointer
30 elif sums3 < 0:
31 left += 1
32 # Else, update the right pointer
33 else:
34 right -= 1
35
36 # Convert the triplets list to a set to remove duplicates, and then convert it back to a list
37 triplets = list(set(triplets))
38 # Return the triplets list
39 return triplets
The time complexity of the above code is O(n^2) and the space complexity is O(n).
Container With Most Water
You are given an integer array height of length n. There are n vertical lines drawn such that the two endpoints of the ith line are (i, 0) and (i, height[i]).
Find two lines that together with the x-axis form a container, such that the container contains the most water. Return the maximum amount of water a container can store.
Notice that you may not slant the container.
1Input: height = [1,8,6,2,5,4,8,3,7]
2Output: 49
3Explanation: The above vertical lines are represented by array [1,8,6,2,5,4,8,3,7]. In this case, the max area of water (blue section) the container can contain is 49.
1class Solution:
2 def maxArea(self, height: List[int]) -> int:
3 # Initialize left and right pointers at the start and end of the list
4 left = 0
5 right = len(height) - 1
6
7 # Initialize the maximum area to 0
8 max_area = 0
9
10 # Loop through the list while the left pointer is less than the right pointer
11 while left < right:
12 # Calculate the width of the rectangle by subtracting the left pointer from the right pointer
13 w = right - left
14
15 # Calculate the height of the rectangle by taking the minimum of the values at the left and right pointers
16 h = min(height[left], height[right])
17
18 # Calculate the area of the rectangle by multiplying the height and width
19 area = h * w
20
21 # Update the maximum area by comparing the current area to the previous maximum
22 max_area = max(max_area, area)
23
24 # If the value at the left pointer is less than the value at the right pointer, move the left pointer right
25 # Otherwise, move the right pointer left
26 if height[left] < height[right]:
27 left += 1
28 else:
29 right -= 1
30
31 # Return the maximum area
32 return max_area
The time complexity of this code is O(n), where n is the length of the height list. This is because the left and right pointers are iterated over the list once, and in each iteration the pointers move either left or right by one position.
The space complexity of this code is O(1), because the space used by the code is constant and does not depend on the size of the input. The only variables that are created are a few integers, which have a constant size regardless of the input size.
Sum of Two Integers
Given two integers a and b, return the sum of the two integers without using the operators + and -
1Input: a = 1, b = 2
2Output: 3
1class Solution:
2 def getSum(self, a, b):
3 # If b is zero, return a
4 if b == 0:
5 return a
6
7 # Calculate the sum of a and b without considering the carry
8 sum_w_carry = a ^ b
9
10 # Calculate the carry
11 carry = (a & b) << 1
12
13 # Return the sum of a and b
14 return self.getSum(sum_w_carry, carry)
The time complexity of the code is O(n), where n is the number of bits needed to represent the numbers a and b in binary. This is because the time complexity of the code is directly proportional to the number of bits needed to represent a and b.
The space complexity of the code is O(n), where n is the maximum depth of the recursion stack. This is because at each recursive call, a new frame is added to the stack, and the maximum depth of the stack is equal to the number of bits needed to represent the numbers a and b in binary.
Number of 1 Bits
Write a function that takes an unsigned integer and returns the number of '1' bits it has (also known as the Hamming weight).
1Input: n = 00000000000000000000000000001011
2Output: 3
3Explanation: The input binary string 00000000000000000000000000001011 has a total of three '1' bits.
1class Solution:
2 def hammingWeight(self, n: int) -> int:
3 # Initialize a count variable to keep track of the number of bits in n that are set to 1
4 count = 0
5
6 # Loop until n is 0
7 while n != 0:
8 # Check if the least significant bit of n is set to 1
9 # If it is, increment count by 1
10 count += n & 1
11
12 # Shift the bits in n to the right by 1
13 # This effectively divides n by 2 and discards any remainder
14 n >>= 1
15
16 # Return the final value of count as the result
17 return count
18
19 # another approach using built-in bin
20 # return bin(n).count('1')
The time complexity of the code is linear in the number of bits in the binary representation of n. This is because the loop continues until n is equal to 0, and the number of bits in the binary representation of n determines how many times the loop will run. Therefore, the time complexity of the code is O(b), where b is the number of bits in the binary representation of n.
The space complexity of the code is constant. This is because the only variable that is used to store any data is the count variable, which does not depend on the input n and always takes up the same amount of space. Therefore, the space complexity of the code is O(1).
Counting Bits
Given an integer n, return an array ans of length n + 1 such that for each i (0 <= i <= n), ans[i] *is the number of* 1*'s in the binary representation of* i.
1Input: n = 5
2Output: [0,1,1,2,1,2]
3Explanation:
40 --> 0
51 --> 1
62 --> 10
73 --> 11
84 --> 100
95 --> 101
1class Solution:
2 def countBits(self, n: int) -> List[int]:
3 # create an array with n+1 elements
4 # to store the number of bits of each number from 0 to n
5 ans = [0] * (n + 1)
6 # loop through each number from 1 to n
7 for i in range(1, n + 1):
8 # find the number of bits of i by dividing i by 2
9 # and storing the result in the index i in the array
10 # this is done by right-shifting the binary representation of i by 1 bit
11 # which is equivalent to dividing i by 2
12 ans[i] = ans[i >> 1]
13 # add the remainder of the division by 2 to the number of bits of i
14 # this is done by performing a bitwise AND operation between i and 1
15 # the result is either 0 or 1 depending on the least significant bit of i
16 # if the least significant bit of i is 0, the result is 0
17 # if the least significant bit of i is 1, the result is 1
18 ans[i] += (i & 1)
19 return ans
20
21 # return [bin(i).count('1') for i in range(n + 1)]
The time complexity of the solution is also O(n) because the loop runs n times, and the operations inside the loop have a constant time complexity. Therefore, the overall time complexity of the solution is O(n).
The space complexity of the solution is O(n) because the size of the array ans is directly proportional to the input n.
Missing Number
Given an array nums containing n distinct numbers in the range [0, n], return the only number in the range that is missing from the array.
1Input: nums = [3,0,1]
2Output: 2
3Explanation: n = 3 since there are 3 numbers, so all numbers are in the range [0,3]. 2 is the missing number in the range since it does not appear in nums.
1class Solution:
2 def missingNumber(self, nums: List[int]) -> int:
3 # get the length of the nums list
4 nums_len = len(nums)
5
6 # create an empty list to store all numbers from 0 to nums_len
7 all_nums = []
8
9 # iterate over the range of 0 to nums_len, inclusive
10 for i in range(0, nums_len+1):
11 # add each number in the range to the all_nums list
12 all_nums.append(i)
13
14 # create a set of all_nums and the nums list
15 # the set of all_nums will contain the missing number
16 missing_num = set(all_nums) ^ set(nums)
17
18 # return the first (and only) element in the set missing_num
19 return next(iter(missing_num))
The time complexity of the above code is O(n), where n is the length of the nums list. This is because we iterate over the nums list once to find the missing number.
The space complexity of the above code is also O(n), because we create a list of length n to store all numbers from 0 to n. Additionally, we create a set of length n, so the overall space complexity is O(n).
Reverse Bits
Reverse bits of a given 32 bits unsigned integer.
1Input: n = 00000010100101000001111010011100
2Output: 964176192 (00111001011110000010100101000000)
3Explanation: The input binary string 00000010100101000001111010011100 represents the unsigned integer 43261596, so return 964176192 which its binary representation is 00111001011110000010100101000000.
1class Solution:
2 def reverseBits(self, n: int) -> int:
3 # Initialize the result to 0
4 ans = 0
5
6 # Loop through the 32 bits in the integer
7 for i in range(32):
8 # Add the last bit of n to the result and shift it left by 1
9 # This puts the next bit in the last bit position
10 ans = (ans << 1) + (n & 1)
11
12 # Shift n right by 1 to get the next bit
13 n >>= 1
14
15 # Return the reversed bits
16 return ans
The time complexity of the above code is O(1), because the number of operations performed is constant and does not depend on the input size. This is because the code always performs the same number of iterations (32) and the number of operations per iteration is also constant.
The space complexity of the above code is also O(1), because the amount of memory used does not depend on the input size. This is because the only variable that is allocated memory is ans, which has a fixed size of 32 bits regardless of the input size.
Climbing Stairs
You are climbing a staircase. It takes n steps to reach the top.
Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?
1Input: n = 3
2Output: 3
3Explanation: There are three ways to climb to the top.
41. 1 step + 1 step + 1 step
52. 1 step + 2 steps
63. 2 steps + 1 step
1from functools import lru_cache
2
3class Solution:
4 # Decorate the climbStairs method with lru_cache
5 # to enable memoization
6 @lru_cache
7 def climbStairs(self, n: int) -> int:
8 # If n is less than 3, return n
9 # This covers the cases where n is 0, 1, or 2
10 if n < 3:
11 return n
12
13 # Otherwise, return the sum of the number of ways to climb
14 # n - 1 stairs and n - 2 stairs
15 else:
16 return self.climbStairs(n-1) + self.climbStairs(n-2)
The time complexity of the above code is O(n), because the number of operations performed depends on the input size. This is because the climbStairs method is called recursively, and the number of recursive calls grows linearly with the input size.
The space complexity of the above code is also O(n), because the amount of memory used depends on the input size. This is because the lru_cache decorator stores the results of each climbStairs call in a cache, and the size of the cache grows linearly with the input size.
Coin Change
You are given an integer array coins representing coins of different denominations and an integer amount representing a total amount of money.
Return the fewest number of coins that you need to make up that amount. If that amount of money cannot be made up by any combination of the coins, return -1.
You may assume that you have an infinite number of each kind of coin.
1Input: coins = [1,2,5], amount = 11
2Output: 3
3Explanation: 11 = 5 + 5 + 1
1class Solution:
2 def coinChange(self, coins: List[int], amount: int) -> int:
3 # Initialize an empty list to store the combinations
4 result = []
5
6 # Define a helper function to search for combinations of coins
7 def dfs(current_combination, current_sum, idx):
8 # If the current combination sums to the target amount,
9 # append it to the result and return
10 if current_sum == amount:
11 result.append(current_combination)
12 return None
13
14 # If the current combination sums to more than the target amount,
15 # return without adding it to the result
16 elif current_sum > amount:
17 return None
18
19 # Recursively search for combinations of coins
20 for i in range(len(coins)):
21 dfs(current_combination + [coins[i]], current_sum + coins[i], i)
22
23 # Call the helper function to search for combinations
24 dfs([], 0, 0)
25
26 # If no combinations were found, return -1
27 if not result:
28 return -1
29
30 # Otherwise, return the length of the shortest combination
31 min_length = min(result, key=len)
32 return len(min_length)
The time complexity of the above code is O(n^m), where n is the number of coins and m is the target amount, because the number of operations performed depends on the product of the input sizes. This is because the dfs function is called recursively, and each recursive call generates n additional calls. Since the number of recursive calls grows exponentially with the input size, the time complexity is O(n^m).
The space complexity of the above code is O(m), because the amount of memory used depends on the target amount. This is because the result list stores combinations of coins, and the maximum number of combinations is equal to the target amount. Additionally, the dfs function uses a constant amount of memory for each recursive call. Therefore, the space complexity is O(m).
Longest Increasing Subsequence
Given an integer array nums, return *the length of the longest strictly increasing*.
1Input: nums = [10,9,2,5,3,7,101,18]
2Output: 4
3Explanation: The longest increasing subsequence is [2,3,7,101], therefore the length is 4.
1def lengthOfLIS2(self, nums: List[int]) -> int:
2 # Define a helper function that uses binary search to find the index
3 # of the target in the array, or if the target is not in the array,
4 # it returns the index where it should be inserted to maintain the order of the array.
5 def binary_search(lis, target):
6 left, right = 0, len(lis) - 1
7 while left <= right:
8 mid = (left + right) // 2
9 if lis[mid] == target:
10 return mid
11 elif lis[mid] < target:
12 left = mid + 1
13 else:
14 right = mid - 1
15 return left
16
17 # Initialize the LIS as an empty list
18 lis = []
19
20 # Iterate through each element in the input array
21 for num in nums:
22 # If the LIS is empty or the current element is greater than the last element in the LIS,
23 # append the current element to the end of the LIS.
24 if not lis or num > lis[-1]:
25 lis.append(num)
26 # Otherwise, update the value in the LIS at the index returned by the binary search function
27 # to the current element. This maintains the order of the LIS and potentially replaces
28 # a smaller element with the current element, which could result in a longer LIS.
29 else:
30 lis[binary_search(lis, num)] = num
31
32 # Return the length of the LIS
33 return len(lis)
The time complexity of the code is O(n * log n), where n is the length of the input list nums. This is because the time complexity of the binary search is O(log n) and it is called n times, once for each element in nums.
The space complexity of the code is O(n), where n is the length of the input list nums. This is because the lis array will store up to n elements at any given time.
Longest Common Subsequence
Given two strings text1 and text2, return the length of their longest common subsequence. If there is no common subsequence, return 0.
1Input: text1 = "abcde", text2 = "ace"
2Output: 3
3Explanation: The longest common subsequence is "ace" and its length is 3.
1class Solution:
2
3 def longestCommonSubsequence(self, text1: str, text2: str) -> int:
4 # Define the helper function with lru_cache
5 @lru_cache(maxsize=None)
6 def lcs_helper(i, j):
7 # If we have reached the end of one of the input strings, return 0
8 if i == len(text1) or j == len(text2):
9 return 0
10 # If the characters at the current positions in the two input strings are the same,
11 # add 1 to the result and move on to the next characters in both strings
12 if text1[i] == text2[j]:
13 return 1 + lcs_helper(i + 1, j + 1)
14 # Otherwise, return the maximum of the two possible next steps
15 return max(lcs_helper(i + 1, j), lcs_helper(i, j + 1))
16
17 # Return the result of calling the helper function with the starting indices (0, 0)
18 return lcs_helper(0, 0)
The time and space complexity of the code depend on the size of the input strings text1 and text2. Because the function uses memoization with lru_cache, the time complexity is effectively O(n * m), where n and m are the lengths of text1 and text2, respectively. The space complexity is also O(n * m) because the lru_cache stores the results of the function calls in a dictionary, which takes up space proportional to the number of function calls made.
Word Break Problem
Given a string s and a dictionary of strings wordDict, return true if s can be segmented into a space-separated sequence of one or more dictionary words.
Note that the same word in the dictionary may be reused multiple times in the segmentation.
1Input: s = "leetcode", wordDict = ["leet","code"]
2Output: true
3Explanation: Return true because "leetcode" can be segmented as "leet code".
1class Solution:
2 def wordBreak(self, s, wordDict):
3 # Create a list to store the results of subproblems
4 dp = [False] * (len(s) + 1)
5 # The empty string can be formed by using words from the dictionary
6 dp[0] = True
7
8 # Loop through all substrings of the input string
9 for i in range(1, len(s) + 1):
10 # Loop through all possible starting positions of the current substring
11 for j in range(i):
12 # If the substring starting at position j can be formed using words from the dictionary,
13 # and the current substring can be formed by appending a word from the dictionary to the
14 # substring starting at position j, then the current substring can be formed using words
15 # from the dictionary
16 if dp[j] and s[j: i] in wordDict:
17 dp[i] = True
18 # We can stop looking for other starting positions once we find one that works
19 break
20
21 # Return the result for the entire input string
22 return dp[-1]
The time complexity of the code is O(n^2), where n is the length of the input string s, because the two for loops iterate over substrings of s. The space complexity is also O(n) because the dp array takes up space proportional to the length of s.
Combination Sum
Given an array of distinct integers nums and a target integer target, return the number of possible combinations that add up to target.
1Input: nums = [1,2,3], target = 4
2Output: 7
3Explanation:
4The possible combination ways are:
5(1, 1, 1, 1)
6(1, 1, 2)
7(1, 2, 1)
8(1, 3)
9(2, 1, 1)
10(2, 2)
11(3, 1)
12Note that different sequences are counted as different combinations.
1def combinationSum4(self, nums: List[int], target: int) -> int:
2 # Initialize a dictionary with the base case
3 dp = {0: 1}
4
5 # Loop through all numbers from 1 to the target value
6 for i in range(1, target + 1):
7 # For each number, sum up the number of ways to make that value using the numbers in the nums list
8 dp[i] = sum(dp.get(i - num, 0) for num in nums)
9
10 # Return the number of ways to make the target value
11 return dp[target]
The time complexity of the above code is O(target * n), where n is the length of the nums list. This is because the inner for loop iterates through all numbers from 1 to the target, and for each number it sums up the number of ways to make that value using the numbers in the nums list, which takes O(n) time.
The space complexity is O(target), because the dp dictionary stores the number of ways to make each value from 0 to the target value, and there are a total of target + 1 entries in the dictionary.
House Robber
You are a professional robber planning to rob houses along a street. Each house has a certain amount of money stashed, the only constraint stopping you from robbing each of them is that adjacent houses have security systems connected and it will automatically contact the police if two adjacent houses were broken into on the same night.
Given an integer array nums representing the amount of money of each house, return *the maximum amount of money you can rob tonight without alerting the police*.
1Input: nums = [1,2,3,1]
2Output: 4
3Explanation: Rob house 1 (money = 1) and then rob house 3 (money = 3).
4Total amount you can rob = 1 + 3 = 4.
1class Solution:
2 def rob(self, nums: List[int]) -> int:
3 # Initialize variables to store the maximum amount of money that can be robbed at the current and previous houses
4 rob, rob2 = 0, 0
5
6 # For each house, find the maximum amount of money that can be robbed at the current house
7 for num in nums:
8 # The maximum amount of money that can be robbed at the current house is the maximum of the sum of the money
9 # from the previous house and the value of the current house, and the maximum amount of money that can be
10 # robbed at the previous house
11 rob, rob2 = rob2, max(rob + num, rob2)
12
13 # Return the maximum amount of money that can be robbed at the last house
14 return rob2
The time complexity of the above code is O(n), where n is the length of the nums list. This is because the for loop iterates through all numbers in the list and performs a constant number of operations on each iteration.
The space complexity is O(1), because the nums list is modified in place and no additional space is used.
House Robber II
You are a professional robber planning to rob houses along a street. Each house has a certain amount of money stashed. All houses at this place are arranged in a circle. That means the first house is the neighbor of the last one. Meanwhile, adjacent houses have a security system connected, and it will automatically contact the police if two adjacent houses were broken into on the same night.
Given an integer array nums representing the amount of money of each house, return *the maximum amount of money you can rob tonight without alerting the police*.
1Input: nums = [2,3,2]
2Output: 3
3Explanation: You cannot rob house 1 (money = 2) and then rob house 3 (money = 2), because they are adjacent houses.
1class Solution:
2 # This method finds the maximum amount of money that can be robbed from the houses in the given list of numbers
3 # It returns the maximum amount of money that can be robbed
4 def rob(self, nums: List[int]) -> int:
5 # If there is only one house, the maximum amount of money that can be robbed is the value of that house
6 if len(nums) == 1:
7 return nums[0]
8
9 # Otherwise, find the maximum amount of money that can be robbed if the first or last house is not robbed
10 # Return the maximum of these two values
11 return max(self.rob1(nums[:-1]), self.rob1(nums[1:]))
12
13
14 # This method finds the maximum amount of money that can be robbed from the houses in the given list of numbers
15 # It returns the maximum amount of money that can be robbed
16 def rob1(self, nums: List[int]) -> int:
17 # Initialize variables to store the maximum amount of money that can be robbed at the current and previous houses
18 rob1, rob2 = 0, 0
19
20 # For each house, find the maximum amount of money that can be robbed at the current house
21 for num in nums:
22 # The maximum amount of money that can be robbed at the current house is the maximum of the sum of the money
23 # from the previous house and the value of the current house, and the maximum amount of money that can be
24 # robbed at the previous house
25 rob1, rob2 = rob2, max(rob1 + num, rob2)
26
27 # Return the maximum amount of money that can be robbed at the last house
28 return rob2
The time complexity of the above code is O(n), where n is the number of houses in the given list of numbers. This is because the rob1() method iterates through the entire list of houses, and the rob() method calls the rob1() method twice, each time with a list of houses that has a length of n-1.
The space complexity of the above code is O(1), because the rob1() method only uses a constant amount of additional memory to store the variables rob1 and rob2.
Decode Ways
Given a string s containing only digits, return the number of ways to decode it.
A message containing letters from A-Z can be encoded into numbers using the following mapping:
1'A' -> "1"
2'B' -> "2"
3...
4'Z' -> "26"
To decode an encoded message, all the digits must be grouped then mapped back into letters using the reverse of the mapping above (there may be multiple ways). For example, "11106" can be mapped into:
"AAJF"with the grouping(1 1 10 6)"KJF"with the grouping(11 10 6)
Note that the grouping (1 11 06) is invalid because "06" cannot be mapped into 'F' since "6" is different from "06".
1Input: s = "12"
2Output: 2
3Explanation: "12" could be decoded as "AB" (1 2) or "L" (12).
1class Solution:
2 def numDecodings(self, s: str) -> int:
3 # If the string is empty or None, there are no possible decodings
4 if len(s) == 0 or s is None:
5 return 0
6
7 # Define a recursive function that uses memoization to improve performance
8 @lru_cache(maxsize=None)
9 def dfs(st):
10 # If the string is empty, there is only one possible decoding
11 if len(st) == 0:
12 return 1
13 # If the string starts with a zero, there are no possible decodings
14 if st[0] == "0":
15 return 0
16 # If the string has only one character, there is only one possible decoding
17 if len(st) == 1:
18 return 1
19 # If the first two characters of the string can be decoded together (i.e. are less than or equal to 26),
20 # then we can consider both decodings: one that decodes the first two characters together, and one that
21 # decodes the first character by itself. Otherwise, we can only consider the single decoding that decodes
22 # the first character by itself.
23 if int(st[:2]) <= 26:
24 return dfs(st[1:]) + dfs(st[2:])
25 else:
26 return dfs(st[1:])
27
28 # Call the recursive function with the original string and return the result
29 return dfs(s)
The time complexity of the above code is O(2^n), where n is the length of the input string. This is because each recursive call branches into two additional recursive calls, and each branch is considered independently. This means that for a string of length n, there will be 2^n total recursive calls.
The space complexity of the above code is O(n), where n is the length of the input string. This is because the dfs function uses memoization to store the results of previous recursive calls, and the memoization table will store at most one result for each possible input string. Since the length of the input string determines the number of possible input strings, the space complexity is O(n).
Jump Game
You are given an integer array nums. You are initially positioned at the array's first index, and each element in the array represents your maximum jump length at that position.
Return true if you can reach the last index, or false otherwise.
1Input: nums = [2,3,1,1,4]
2Output: true
3Explanation: Jump 1 step from index 0 to 1, then 3 steps to the last index.
1class Solution:
2 # greedy approach
3 def canJump(self, nums: List[int]) -> bool:
4 goal = len(nums) - 1 # last index
5
6 # for i in reversed(range(goal)):
7 for idx in range(goal, -1, -1):
8 if idx + nums[idx] >= goal:
9 # we have added the current index to the jump length,
10 # because at any given index, futhest we can reach is the current index + jump length
11 goal = idx
12
13 # return True if goal == 0 else False
14 return goal == 0
The time complexity of the code is O(n), where n is the length of the nums list, because the for loop iterates over all elements in the list.
The space complexity of the code is O(1), because the number of variables used does not depend on the size of the input and remains constant. The variables used are goal (1 variable), idx (1 variable), and nums (1 variable, which references the input list and is not counted as a separate variable in the space complexity calculation).
Course Schedule
There are a total of numCourses courses you have to take, labeled from 0 to numCourses - 1. You are given an array prerequisites where prerequisites[i] = [ai, bi] indicates that you must take course bi first if you want to take course ai.
- For example, the pair
[0, 1], indicates that to take course0you have to first take course1.
Return true if you can finish all courses. Otherwise, return false.
1Input: numCourses = 2, prerequisites = [[1,0]]
2Output: true
3Explanation: There are a total of 2 courses to take.
4To take course 1 you should have finished course 0. So it is possible.
1class Solution:
2 # video explanation: https://youtu.be/EgI5nU9etnU
3 def canFinish(self, numCourses: int, prerequisites: List[List[int]]) -> bool:
4 # define a adjacency list to represent the graph and store the prerequisites
5 # put empty list for each node initially
6 # keys: course number
7 # values: list of prerequisites
8 adj_map = {i: [] for i in range(numCourses)}
9 # {0: [], 1: []}
10
11 # add the prerequisites to the adjacency list
12 # c: course, p: prerequisites
13 for c, p in prerequisites:
14 # add course as key and pre_req as value
15 adj_map[c].append(p)
16
17 # adj_map = {0: [1], 1: [0]}
18
19 # track the visited nodes to check if there is a cycle
20 visited = set()
21
22 # apply dfs to determine if there is a cycle
23 # v: course, adj_map: adjacency list
24 # stack, because we are implementing dfs
25 def hasCycle(v, stack):
26 # if the node is already visited, return true
27 if v in visited:
28 if v in stack:
29 return True
30 return False
31
32 # mark the node as visited
33 visited.add(v)
34 # add the node to the stack
35 stack.append(v)
36
37 # check if there is a cycle in the graph
38 # check for all values in the adjacency list of the node
39 for pre_req in adj_map[v]:
40 if hasCycle(pre_req, stack):
41 return True
42
43 # remove the node from the stack
44 stack.pop()
45 return False
46
47 # check if there is a cycle in the graph
48 for v in range(numCourses):
49 if hasCycle(v, []):
50 # if hasCycle returns true, there is a cycle,
51 # so we cannot finish all courses
52 return False
53
54 return True
The time complexity of the code is O(V+E), where V is the number of courses (vertices) and E is the number of prerequisites (edges). This is because the hasCycle function is called once for each course, and for each course, it visits all of its prerequisites, at most once.
The space complexity of the code is O(V), because at most, the call stack will contain all the courses.
Number of Islands
Given an m x n 2D binary grid grid which represents a map of '1's (land) and '0's (water), return the number of islands.
An island is surrounded by water and is formed by connecting adjacent lands horizontally or vertically. You may assume all four edges of the grid are all surrounded by water.
1Input: grid = [
2 ["1","1","1","1","0"],
3 ["1","1","0","1","0"],
4 ["1","1","0","0","0"],
5 ["0","0","0","0","0"]
6]
7Output: 1
1class Solution:
2 # video explanation: https://youtu.be/ZixJexAaOAk?t=474
3 def numIslands(self, grid: List[List[str]]) -> int:
4
5 # number of rows
6 rows = len(grid)
7 # number of cols
8 cols = len(grid[0])
9
10 count = 0
11
12 for i in range(rows):
13 for j in range(cols):
14 if grid[i][j] == "1":
15 self.dfs(i, j, rows, cols, grid)
16 count += 1
17 return count
18
19 def dfs(self, i, j, rows, cols, grid):
20 # This is checking if the current index is out of bounds or if the current index is not a 1.
21 if i >= rows or i < 0 or j >= cols or j < 0 or grid[i][j] == "0":
22 return 0
23
24 # Use # that modifies the input to ensure that the count isn't incremented where we could accidentally
25 # traverse the same '1' cell multiple times and get into an infinite loop within an island
26 # it's basically a implicit way of marking the visited square/nodes instead of putting the
27 # visited nodes in an visited array
28 grid[i][j] = "0"
29
30 # top
31 self.dfs(i, j + 1, rows, cols, grid)
32 # bottom
33 self.dfs(i, j - 1, rows, cols, grid)
34 # left
35 self.dfs(i - 1, j, rows, cols, grid)
36 # right
37 self.dfs(i + 1, j, rows, cols, grid)
The time complexity of the code is O(R x C), where R is the number of rows and C is the number of columns in the grid. This is because the dfs function is called once for each cell in the grid, and for each cell, it visits all of its neighbors, at most once.
The space complexity of the code is O(R x C), because at most, the call stack will contain all the cells in the grid.
Insert Interval
You are given an array of non-overlapping intervals intervals where intervals[i] = [starti, endi] represent the start and the end of the ith interval and intervals is sorted in ascending order by starti. You are also given an interval newInterval = [start, end] that represents the start and end of another interval.
Insert newInterval into intervals such that intervals is still sorted in ascending order by starti and intervals still does not have any overlapping intervals (merge overlapping intervals if necessary).
Return intervals after the insertion.
1Input: intervals = [[1,3],[6,9]], newInterval = [2,5]
2Output: [[1,5],[6,9]]
1class Solution:
2 def insert(self, intervals: List[List[int]], newInterval: List[int]) -> List[List[int]]:
3 # Add the new interval to the list of intervals
4 intervals.append(newInterval)
5 # Sort the intervals by their start time
6 intervals.sort(key=lambda x: x[0])
7
8 # Initialize the output list with the first interval in the sorted list
9 output = [intervals[0]]
10 # Iterate over the remaining intervals in the sorted list
11 for i in range(1, len(intervals)):
12 # If the current interval overlaps with the last interval in the output list
13 # Update the last interval in the output list to include the current interval
14 if intervals[i][0] <= output[-1][1]:
15 output[-1][1] = max(output[-1][1], intervals[i][1])
16 # If the current interval doesn't overlap with the last interval in the output list
17 # Add the current interval to the output list
18 else:
19 output.append(intervals[i])
20
21 # Return the output list
22 return output
The time complexity of the code is O(N log N), where N is the number of intervals. This is because sorting the intervals takes O(N log N) time and the remaining operations take O(N) time.
The space complexity of the code is O(N), because at most, the output list will contain all the intervals.
Merge Intervals
Given an array of intervals where intervals[i] = [starti, endi], merge all overlapping intervals, and return an array of the non-overlapping intervals that cover all the intervals in the input.
1Input: intervals = [[1,3],[2,6],[8,10],[15,18]]
2Output: [[1,6],[8,10],[15,18]]
3Explanation: Since intervals [1,3] and [2,6] overlap, merge them into [1,6].
1class Solution:
2
3 # This function takes a list of intervals as input and returns a list of
4 # intervals with overlapping intervals merged.
5 # The intervals are sorted by their starting coordinate before merging.
6 def merge(self, intervals: List[List[int]]) -> List[List[int]]):
7
8 # sort the intervals by their starting coordinate
9 intervals.sort(key=lambda x: x[0])
10
11 # initialize the output with the first interval in the sorted list
12 output = [intervals[0]]
13
14 # iterate through the rest of the intervals in the sorted list
15 for i in range(1, len(intervals)):
16
17 # if the current interval's start coordinate is less than or equal to the
18 # end coordinate of the last interval in the output list
19 # then the two intervals overlap and need to be merged
20 if intervals[i][0] <= output[-1][1]:
21
22 # merge the current interval with the last interval in the output list
23 # by updating the end coordinate of the last interval
24 # with the maximum of its current value and the end coordinate of the current interval
25 output[-1][1] = max(output[-1][1], intervals[i][1])
26
27 # if the current interval's start coordinate is greater than the end coordinate
28 # of the last interval in the output list
29 # then the two intervals do not overlap and the current interval can be added to the output list as is
30 else:
31 output.append(intervals[i])
32
33 # return the list of merged intervals
34 return output
The time complexity of the code is O(n _ log(n)), where n is the number of intervals in the input list. This is because the intervals are sorted by their starting coordinate using the sort() method, which has a time complexity of O(n _ log(n)).
The space complexity of the code is O(n), where n is the number of intervals in the input list. This is because the output list is constructed by iterating through the input list and adding intervals to it, which requires storing a total of n intervals in the output list.
Reverse Linked List
Given the head of a singly linked list, reverse the list, and return the reversed list.
1Input: head = [1,2,3,4,5]
2Output: [5,4,3,2,1]
1class Solution:
2 def reverseList(self, head: Optional[ListNode]) -> Optional[ListNode]:
3 """
4 - The linked list is reversed in place, so no additional space is used for the reversed list.
5 - The function works by iterating through the linked list and reversing the links between the nodes.
6 - The original head of the list becomes the tail of the reversed list, and the original tail becomes the head.
7 """
8
9 # Initialize the previous node as None and the current node as the head of the list
10 previous, current = None, head
11
12 # Iterate through the linked list until we reach the end
13 while current:
14 # Reverse the link by pointing the current node's next reference to the previous node
15 # Then, update the previous node to the current node and the current node to the next node in the list
16 current.next, previous, current = previous, current, current.next
17
18 # Return the previous node, which is now the head of the reversed list
19 return previous
The time complexity of the above code is O(n), where n is the number of nodes in the linked list. This is because the function iterates through the entire linked list once to reverse the links between the nodes.
The space complexity of the above code is O(1), as the function reverses the linked list in place and does not use any additional space. It only uses a few variables (previous, current) to store references to nodes in the linked list.
Linked List Cycle
Given head, the head of a linked list, determine if the linked list has a cycle in it.
There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the next pointer. Internally, pos is used to denote the index of the node that tail's next pointer is connected to. Note that pos is not passed as a parameter.
Return true if there is a cycle in the linked list. Otherwise, return false.
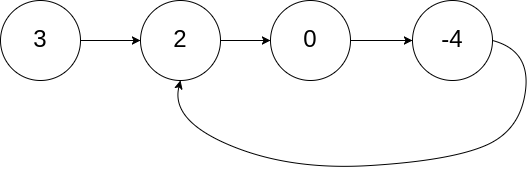
1Input: head = [3,2,0,-4], pos = 1
2Output: true
3Explanation: There is a cycle in the linked list, where the tail connects to the 1st node (0-indexed).
1class Solution:
2 def hasCycle(self, head: Optional[ListNode]) -> bool:
3 """
4 - A linked list has a cycle if any node in the list appears more than once.
5 - This function uses the "Floyd's cycle-finding algorithm", also known as the "tortoise and hare algorithm".
6 - It uses two pointers, "slow" and "fast", that move through the linked list at different speeds.
7 - If there is a cycle, the fast pointer will eventually catch up to the slow pointer.
8 """
9
10 # Initialize both pointers to the head of the linked list
11 slow = fast = head
12
13 # Iterate through the linked list until the fast pointer reaches the end
14 while fast and fast.next:
15 # Move the slow pointer one node at a time
16 slow = slow.next
17 # Move the fast pointer two nodes at a time
18 fast = fast.next.next
19
20 # If the slow and fast pointers are pointing to the same node, there is a cycle in the linked list
21 if slow == fast:
22 return True
23
24 # If the fast pointer reached the end of the linked list, there is no cycle
25 return False
The time complexity of the above code is O(n), where n is the number of nodes in the linked list. In the worst case, the fast pointer will iterate through the entire linked list and the slow pointer will iterate through half of the linked list.
The space complexity of the above code is O(1), as the function only uses a few variables (slow, fast) to store references to nodes in the linked list and does not use any additional space.
Merge Two Sorted Lists
You are given the heads of two sorted linked lists list1 and list2.
Merge the two lists in a one sorted list. The list should be made by splicing together the nodes of the first two lists.
Return the head of the merged linked list.
1Input: list1 = [1,2,4], list2 = [1,3,4]
2Output: [1,1,2,3,4,4]
1class Solution:
2 def mergeTwoLists(self, list1: Optional[ListNode], list2: Optional[ListNode]) -> Optional[ListNode]:
3 """
4 - This function uses recursion to repeatedly merge the two linked lists, starting with the smallest nodes.
5 - If either of the input lists is empty, the function returns the other list.
6 - Otherwise, it compares the values of the two list heads and appends the smaller one to the merged list.
7 """
8
9 # If either of the lists is empty, return the other list
10 if not list1 or not list2:
11 return list1 or list2
12
13 # Compare the values of the two list heads
14 # If the value of list1 is smaller, set the next node of list1 to the result of merging the next
15 # nodes of list1 and list2
16 # Otherwise, set the next node of list2 to the result of merging list1 and the next nodes of list2
17 if list1.val < list2.val:
18 list1.next = self.mergeTwoLists(list1.next, list2)
19 return list1
20 else:
21 list2.next = self.mergeTwoLists(list1, list2.next)
22 return list2
The time complexity of the above code is O(n), where n is the total number of nodes in the two linked lists. This is because the function performs a constant amount of work for each node in the lists.
The space complexity of the above code is O(n), as the function uses recursion and the call stack may grow up to the size of the larger of the two input linked lists. However, since the function is merging the linked lists in place and not creating a new list, the space complexity could also be considered O(1).
Spiral Matrix
Given an m x n matrix, return all elements of the matrix in spiral order.
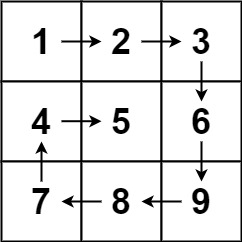
1Input: matrix = [[1,2,3],[4,5,6],[7,8,9]]
2Output: [1,2,3,6,9,8,7,4,5]
1class Solution:
2 def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
3 """
4 - The function iteratively removes the first row of the matrix and
5 - then rotates the remaining matrix 90 degrees clockwise.
6 - This process is repeated until the matrix is empty.
7 """
8
9 result = []
10
11 # While the matrix is not empty
12 while matrix:
13
14 # Add the elements of the first row of the matrix to the result list
15 result.extend(matrix.pop(0))
16
17 # If the matrix is empty, break the loop
18 if not matrix:
19 break
20
21 # Rotate the matrix 90 degrees clockwise
22 # This is done by transposing the matrix and reversing each row
23 matrix = [*zip(*matrix)][::-1]
24
25 # Return the result list
26 return result
The time complexity of the above code is O(n), where n is the total number of elements in the matrix. This is because the function iterates through each element of the matrix once.
The space complexity of the above code is O(n), as the function creates a new list to store the elements of the matrix in spiral order. The size of the list will be the same as the number of elements in the matrix.
Rotate Image
You are given an n x n 2D matrix representing an image, rotate the image by 90 degrees (clockwise).
You have to rotate the image in-place, which means you have to modify the input 2D matrix directly. DO NOT allocate another 2D matrix and do the rotation.
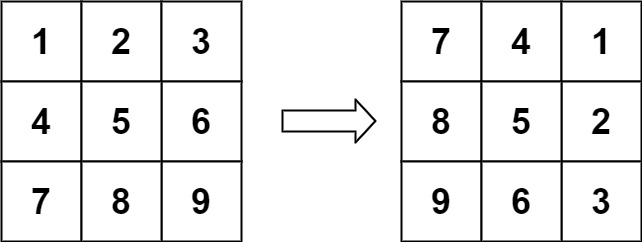
1Input: matrix = [[1,2,3],[4,5,6],[7,8,9]]
2Output: [[7,4,1],[8,5,2],[9,6,3]]
1class Solution:
2 def rotate(self, matrix: List[List[int]]) -> None:
3 """
4 - The function first reverses the matrix horizontally and then transposes it.
5 - Reversing the matrix horizontally is equivalent to rotating it 270 degrees clockwise.
6 - Transposing the matrix swaps the rows and columns, which is equivalent to rotating it 90 degrees clockwise.
7 """
8
9 # Reverse the matrix horizontally
10 matrix.reverse()
11
12 # Transpose the matrix
13 # This is done by swapping the elements at (i, j) and (j, i) for all i and j
14 for i in range(len(matrix)):
15 for j in range(i):
16 matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]
Bonus : rotate the image by 90 degrees (anti-clockwise)
1def rotate(matrix):
2 for i in range(len(matrix) - 1, -1, -1):
3 for j in range(i):
4 matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]
5 matrix.reverse()
The time complexity of the above code is O(n^2), where n is the number of rows and columns in the matrix. This is because the function iterates through each element of the matrix once to reverse it horizontally and again to transpose it.
The space complexity of the above code is O(1), as the function modifies the matrix in place and does not use any additional space.
Word Search
Given an m x n grid of characters board and a string word, return true if word exists in the grid.
The word can be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once.
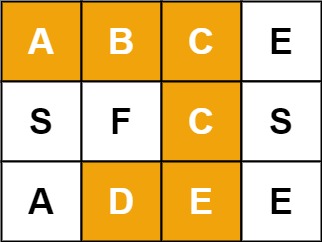
1Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
2Output: true
1class Solution:
2 def exist(self, board: List[List[str]], word: str) -> bool:
3 """
4 - The function uses depth-first search to explore the possible paths through the matrix.
5 - It uses a set, "path", to keep track of the letters that have already been visited.
6 - If the current letter in the matrix matches the current letter in the word,
7 the function continues the search in the four adjacent cells.
8 - If the search reaches the end of the word, the function returns True.
9 - If the search reaches a cell that is out of bounds, already visited,
10 or has a different letter, the function returns False.
11 """
12
13 # Get the number of rows and columns in the matrix
14 rows = len(board)
15 cols = len(board[0])
16
17 # Initialize a set to keep track of the visited cells
18 path = set()
19
20 # Define the recursive function for depth-first search
21 def dfs(r, c, w):
22 # If the search has reached the end of the word, return True
23 if w == len(word):
24 return True
25
26 # If the current cell is out of bounds, already visited, or has a different letter, return False
27 if (
28 r < 0
29 or r >= rows
30 or c < 0
31 or c >= cols
32 or (r, c) in path
33 or word[w] != board[r][c]
34 ):
35 return False
36
37 # Mark the current cell as visited
38 path.add((r, c))
39
40 res = (
41 dfs(r + 1, c, w+1)
42 or dfs(r - 1, c, w+1)
43 or dfs(r, c + 1, w+1)
44 or dfs(r, c - 1, w+1)
45 )
46
47 path.remove((r, c))
48 return res
49
50 for r in range(rows):
51 for c in range(cols):
52 if dfs(r, c, 0):
53 return True
54 return False
The time complexity of the above code is O(nm * 4^k), where n and m are the number of rows and columns in the matrix, respectively, and where k is the length of the word being searched for. This is because at each step of the search, the algorithm has four possible options to choose from: it can move to the cell above, below, to the left, or to the right. If the search continues until it reaches the end of the word, the function will have made 4^k recursive calls.
The space complexity of the above code is O(k), as the function uses a set to store the visited cells, and the size of the set will be at most k.
Word Search II
Given an m x n board of characters and a list of strings words, return all words on the board.
Each word must be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once in a word.
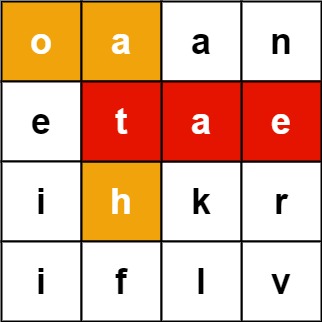
1Input: board = [["o","a","a","n"],["e","t","a","e"],["i","h","k","r"],["i","f","l","v"]], words = ["oath","pea","eat","rain"]
2Output: ["eat","oath"]
1class Solution:
2 def findWords(self, board: List[List[str]], words: List[str]) -> List[str]:
3 # Get the number of rows and columns in the board
4 rows = len(board)
5 cols = len(board[0])
6
7 # Initialize a set to store visited cells during the search
8 path = set()
9
10 # Initialize a set to store the words found in the board
11 result = set()
12
13 def dfs(r, c, w, word):
14 # If we have reached the end of the word, add it to the result set
15 if w == len(word):
16 result.add(word)
17 return
18
19 # If the current cell is out of bounds, already visited, or the
20 # character at the cell does not match the current character in the word,
21 # return without searching further
22 if (
23 r < 0
24 or r >= rows
25 or c < 0
26 or c >= cols
27 or (r, c) in path
28 or word[w] != board[r][c]
29 ):
30 return
31
32 # Add the current cell to the visited set
33 path.add((r, c))
34
35 # Search in all four directions from the current cell
36 dfs(r + 1, c, w + 1, word)
37 dfs(r - 1, c, w + 1, word)
38 dfs(r, c + 1, w + 1, word)
39 dfs(r, c - 1, w + 1, word)
40
41 # Remove the current cell from the visited set
42 path.remove((r, c))
43
44 # Iterate through each cell in the board
45 for r in range(rows):
46 for c in range(cols):
47 # For each word in the list of words, start a depth-first search from
48 # the current cell to find the word in the board
49 for word in words:
50 dfs(r, c, 0, word)
51
52 # Return the list of words found in the board
53 return list(result)
The time complexity of the above code is O(mn * 4^l), where m and n are the number of rows and columns in the board, and l is the length of the longest word in the list of words.
This is because the outer loop runs in O(mn) time, and the inner loop runs in O(l) time. The dfs function is called once for each cell in the board and each character in the word, so it runs in O(4^l) time in the worst case, when the word is not found and the function needs to search in all four directions from each cell.
The space complexity of the code is O(mn + l), as the path set used to store visited cells during the search takes O(mn) space, and the word parameter of the dfs function takes O(l) space.
Longest Substring Without Repeating Characters
Given a string s, find the length of the longest substring without repeating characters.
1Input: s = "abcabcbb"
2Output: 3
3Explanation: The answer is "abc", with the length of 3.
1class Solution:
2 def lengthOfLongestSubstring(self, s: str) -> int:
3 """
4 - The function uses a sliding window approach to keep track of the current substring.
5 - It maintains a set, "char_set", of the characters in the current substring.
6 - It uses two pointers, "left" and "right", to define the boundaries of the window.
7 - If the character at the right pointer is already in the set, the function removes
8 the character at the left pointer and moves it to the right.
9 - The function updates the maximum length of the substring every time the right pointer moves.
10 """
11
12 # initialize an empty set to keep track of the characters in the current substring
13 char_set = set()
14
15 # initialize the left and right pointers
16 left = 0
17 max_len = 0
18
19 # Iterate through the string with the right pointer
20 for right in range(len(s)):
21
22 # While the character at the right pointer is in the set
23 while s[right] in char_set:
24
25 # Remove the character at the left pointer from the set
26 char_set.remove(s[left])
27
28 # Move the left pointer to the right
29 left += 1
30
31 # Add the character at the right pointer to the set
32 char_set.add(s[right])
33
34 # Update the maximum length of the substring
35 max_len = max(max_len, len(char_set))
36
37 # Return the maximum length of the substring
38 return max_len
The time complexity of the above code is O(n), where n is the length of the input string. This is because the function uses a sliding window approach, which involves iterating through the string once with the right pointer and updating the left pointer and the set of characters in the current substring.
The space complexity of the above code is O(k), where k is the size of the set of characters in the current substring. This is because the function uses a set to store the characters in the current substring, and the size of the set will be at most k.
Valid Anagram
Given two strings s and t, return true if t is an anagram of s, and false otherwise.
An Anagram is a word or phrase formed by rearranging the letters of a different word or phrase, typically using all the original letters exactly once.
1Input: s = "anagram", t = "nagaram"
2Output: true
1class Solution:
2 def isAnagram(self, s: str, t: str) -> bool:
3 """
4 - An anagram is a word or phrase formed by rearranging the letters of a different word or phrase.
5 - The function first checks if the two strings have the same length. If not, they cannot be anagrams.
6 - It then sorts both strings and compares the characters at each position.
7 - If any of the characters do not match, the function returns False.
8 - Otherwise, it returns True.
9 """
10
11 # Get the length of the two strings
12 x1 = len(s)
13 x2 = len(t)
14
15 # If the lengths are different, the strings cannot be anagrams
16 if x1 != x2:
17 return False
18
19 # Sort the two strings
20 s = sorted(s)
21 t = sorted(t)
22
23 # Compare the characters at each position
24 for i in range(0,x1):
25 # If any of the characters do not match, return False
26 if s[i] != t[i]:
27 return False
28
29 # If all characters match, return True
30 return True
The time complexity of the above code is O(nlogn), where n is the length of the input strings. This is because the function sorts the two strings using the built-in sorted function, which has a time complexity of O(nlogn).
The space complexity of the above code is O(n), where n is the length of the input strings. This is because the function creates two new sorted strings, which have a combined size of 2n.
Solving the same problem using O(n) time:
1from collections import Counter
2
3class Solution:
4 def isAnagram(self, s: str, t: str) -> bool:
5 return len(s) == len(t) and Counter(s) == Counter(t)
The time complexity of the above code is O(n), where n is the length of the input strings. This is because the function uses the Counter function from the collections module, which has a time complexity of O(n) for constructing the counter objects and a time complexity of O(1) for comparing them.
The space complexity of the above code is O(n), where n is the length of the input strings. This is because the function creates two Counter objects, which have a combined size of 2n.
Group Anagrams
Given an array of strings strs, group the anagrams together. You can return the answer in any order.
An Anagram is a word or phrase formed by rearranging the letters of a different word or phrase, typically using all the original letters exactly once.
1Input: strs = ["eat","tea","tan","ate","nat","bat"]
2Output: [["bat"],["nat","tan"],["ate","eat","tea"]]
1class Solution:
2 def groupAnagrams(self, strs: List[str]) -> List[List[str]]:
3 """
4 - The function creates a dictionary to store the groups of anagrams.
5 - It iterates through the input strings and sorts each string.
6 - If the sorted string is not in the dictionary, it creates a new group with the original string.
7 - If the sorted string is in the dictionary, it appends the original string to the corresponding group.
8 - Finally, it returns the values of the dictionary as a list of lists.
9 """
10
11 # Create a dictionary to store the groups of anagrams
12 anagrams = {}
13
14 # Iterate through the input strings
15 for s in strs:
16 # Sort the string
17 sorted_s = "".join(sorted(s))
18
19 # If the sorted string is not in the dictionary, create a new group with the original string
20 if sorted_s not in anagrams:
21 anagrams[sorted_s] = [s]
22 # If the sorted string is in the dictionary, append the original string to the corresponding group
23 else:
24 anagrams[sorted_s] = [s]
25
26 return list(anagrams.values())
The time complexity of the above code is O(nmlogn), where n is the number of strings in the input list and m is the average length of the strings. This is because the function sorts each string, which has a time complexity of O(mlogn).
The space complexity of the above code is O(nm), where n is the number of strings in the input list and m is the average length of the strings. This is because the function stores each original string in the dictionary, which has a combined size of nm.
Valid Parentheses
Given a string s containing just the characters '(', ')', '{', '}', '[' and ']', determine if the input string is valid.
An input string is valid if:
- Open brackets must be closed by the same type of brackets.
- Open brackets must be closed in the correct order.
- Every close bracket has a corresponding open bracket of the same type.
1Input: s = "()[]{}"
2Output: true
1class Solution:
2 def isValid(self, s: str) -> bool:
3 """
4 - The function uses a stack to store the opening parentheses, brackets, and curly braces.
5 - It iterates through the characters in the string and does the following:
6 - If the character is a closing parenthesis, bracket, or curly brace, it checks if the corresponding
7 opening parenthesis, bracket, or curly brace is at the top of the stack. If not, the string is invalid.
8 - If the character is an opening parenthesis, bracket, or curly brace, it pushes it onto the stack.
9 - If the stack is empty at the end, the string is valid. Otherwise, it is invalid.
10 """
11
12 # Create a dictionary to store the corresponding opening parenthesis, bracket, or curly brace
13 # for each closing parenthesis, bracket, or curly brace
14 m = {
15 ")": "(",
16 "}": "{",
17 "]": "["
18 }
19
20 # Create an empty stack to store the opening parentheses, brackets, and curly braces
21 stack = []
22
23 # Iterate through the characters in the string
24 for c in s:
25 if c in m:
26 if not stack or stack.pop() != m[c]:
27 return False
28 else:
29 stack.append(c)
30
31 return not stack
The time complexity of the above code is O(n), where n is the length of the input string. This is because the function iterates through the characters in the string once.
The space complexity of the above code is O(n), where n is the length of the input string. This is because the function stores the opening parentheses, brackets, and curly braces in a stack, which has a size of n at most.
Valid Palindrome
A phrase is a palindrome if, after converting all uppercase letters into lowercase letters and removing all non-alphanumeric characters, it reads the same forward and backward. Alphanumeric characters include letters and numbers.
Given a string s, return true if it is a palindrome, or false otherwise.
1Input: s = "A man, a plan, a canal: Panama"
2Output: true
3Explanation: "amanaplanacanalpanama" is a palindrome.
1class Solution:
2 def isPalindrome(self, s: str) -> bool:
3 # Convert the string to lowercase
4 s = s.lower()
5
6 # Keep only alphanumeric characters
7 s = [c for c in s if c.isalnum()]
8
9 # Check if the string is a palindrome
10 # by comparing it to its reverse
11 return s == s[::-1]
The time complexity of the above code is O(n), where n is the length of the input string s. This is because the code iterates through the string once to convert it to lowercase and once to filter out non-alphanumeric characters.
The space complexity of the above code is also O(n), as a new list is created that has the same length as the input string. This is because the list comprehension [c for c in s if c.isalnum()] creates a new list that contains all alphanumeric characters from the input string.
Longest Palindromic Substring
Given a string s, return the longest palindromic substring in s.
1Input: s = "babad"
2Output: "bab"
3Explanation: "aba" is also a valid answer.
1class Solution:
2 def longestPalindrome(self, s: str) -> str:
3 # Initialize an empty string to store the longest palindrome found so far
4 longest_palindrome = ""
5
6 # Iterate through each character in the input string
7 for i in range(len(s)):
8 # Check if the substring centered at this character is a palindrome
9 # with an odd length (e.g. "aba")
10 odd_palindrome = self.isPalindrome(s, i, i)
11
12 # Check if the substring centered at this character is a palindrome
13 # with an even length (e.g. "abba")
14 even_palindrome = self.isPalindrome(s, i, i+1)
15
16 # Update the longest palindrome if either of these substrings is longer
17 # than the current longest palindrome
18 if len(odd_palindrome) > len(longest_palindrome):
19 longest_palindrome = odd_palindrome
20 if len(even_palindrome) > len(longest_palindrome):
21 longest_palindrome = even_palindrome
22
23 # Return the longest palindrome found
24 return longest_palindrome
25
26 def isPalindrome(self, s, start, end):
27 # While the start and end indices are within the bounds of the string
28 # and the characters at these indices are equal, move the indices inward
29 while start >= 0 and end < len(s) and s[start] == s[end]:
30 start -= 1
31 end += 1
32
33 # Return the palindrome substring
34 # Note that start and end are now at the indices immediately
35 # before and after the palindrome, so we need to add 1 to start
36 # and subtract 1 from end to get the actual palindrome substring
37 return s[start+1 : end]
The time complexity of the longestPalindrome() method is O(n^2), where n is the length of the input string s. This is because the method iterates through the string once to check for odd-length palindromes and once to check for even-length palindromes, and for each iteration it calls the isPalindrome() method, which has a time complexity of O(n).
The space complexity of the longestPalindrome() method is O(1), as it only stores a few constant-sized variables (e.g. longest_palindrome, odd_palindrome, and even_palindrome).
The time complexity of the isPalindrome() method is O(n), as it iterates through the string once while the indices start and end are within the bounds of the string and the characters at these indices are equal.
The space complexity of the isPalindrome() method is also O(1), as it only stores a few constant-sized variables (e.g. start and end).
Palindromic Substrings
Given a string s, return the number of palindromic substrings in it. A string is a palindrome when it reads the same backward as forward.
A substring is a contiguous sequence of characters within the string.
Example 1:
1Input: s = "abc"
2Output: 3
3Explanation: Three palindromic strings: "a", "b", "c".
Example 2:
1Input: s = "aaa"
2Output: 6
3Explanation: Six palindromic strings: "a", "a", "a", "aa", "aa", "aaa".
1class Solution:
2 def countSubstrings(self, s: str) -> int:
3 # Initialize a counter to keep track of the number of palindromes found
4 palindrome_count = 0
5
6 # Iterate through each character in the input string
7 for i in range(len(s)):
8 # Check for palindromes with odd length (e.g. "aba")
9 palindrome_count += self.expandFromCenter(s, i, i)
10 # Check for palindromes with even length (e.g. "abba")
11 palindrome_count += self.expandFromCenter(s, i, i+1)
12
13 # Return the total number of palindromic substrings
14 return palindrome_count
15
16 def expandFromCenter(self, s, left, right):
17 # Initialize a counter to keep track of the number of palindromes
18 # found while expanding from the center
19 count = 0
20
21 # While the indices are within the bounds of the string
22 # and the characters at these indices are equal,
23 # increment the counter and move the indices outward
24 while left >= 0 and right < len(s) and s[left] == s[right]:
25 count += 1
26 left -= 1
27 right += 1
28
29 # Return the number of palindromes found
30 return count
This solution has a time complexity of O(n^2), as it iterates through the string once to check every possible palindrome substring, and each palindrome check requires another iteration through the string. Its space complexity is O(1), as it does not allocate any additional space beyond a few variables.
Unique Paths
There is a robot on an m x n grid. The robot is initially located at the top-left corner (i.e., grid[0][0]). The robot tries to move to the bottom-right corner (i.e., grid[m - 1][n - 1]). The robot can only move either down or right at any point in time.
Given the two integers m and n, return the number of possible unique paths that the robot can take to reach the bottom-right corner.
The test cases are generated so that the answer will be less than or equal to 2 * 109.
Example 1:
1Input: m = 3, n = 7
2Output: 28
Example 2:
1Input: m = 3, n = 2
2Output: 3
3Explanation: From the top-left corner, there are a total of 3 ways to reach the bottom-right corner:
41. Right -> Down -> Down
52. Down -> Down -> Right
63. Down -> Right -> Down
Solution 1
1class Solution:
2 def uniquePaths(self, m: int, n: int) -> int:
3 # Initialize a 2D array to store the number of paths to reach each cell
4 # The array is initialized to 0
5 path_count = [[0] * n for _ in range(m)]
6
7 # There is only 1 way to reach the first cell
8 path_count[0][0] = 1
9
10 # Iterate through each cell in the grid
11 for i in range(m):
12 for j in range(n):
13 # If we are not in the first row or column, the number of ways
14 # to reach this cell is the sum of the number of ways to reach
15 # the cell above and the cell to the left
16 if i > 0 and j > 0:
17 path_count[i][j] = path_count[i-1][j] + path_count[i][j-1]
18 # If we are in the first row, the number of ways to reach this cell
19 # is the number of ways to reach the cell to the left
20 elif i == 0 and j > 0:
21 path_count[i][j] = path_count[i][j-1]
22 # If we are in the first column, the number of ways to reach this cell
23 # is the number of ways to reach the cell above
24 elif i > 0 and j == 0:
25 path_count[i][j] = path_count[i-1][j]
26
27 # Return the number of ways to reach the bottom-right cell
28 return path_count[m-1][n-1]
This solution has a time complexity of O(mn), as it iterates through the grid once to compute the number of paths to reach each cell. Its space complexity is O(mn), as it stores the number of paths to reach each cell in a 2D array.
Solution 2
1class Solution:
2 def uniquePaths(self, m: int, n: int) -> int:
3 # Initialize a counter to keep track of the number of paths found
4 path_count = 0
5
6 # Recursive function to explore paths from the current cell
7 def dfs(i, j):
8 # If we have reached the bottom-right cell, increment the path count
9 if i == m - 1 and j == n - 1:
10 nonlocal path_count
11 path_count += 1
12 return
13 # If we are not at the bottom-right cell yet, explore paths
14 # going down and right
15 if i < m - 1:
16 dfs(i + 1, j)
17 if j < n - 1:
18 dfs(i, j + 1)
19
20 # Start the search at the top-left cell
21 dfs(0, 0)
22
23 # Return the total number of paths found
24 return path_count
This DFS solution has a time complexity of O(2^(m+n)), as it may explore up to 2 paths from each cell and there are a total of m+n cells in the grid. Its space complexity is O(m+n), as it stores the current cell coordinates and the path count in the function call stack.
Note that the DFS solution may not be efficient for large values of m and n, as the time complexity is exponential. In such cases, the dynamic programming solution may be preferred, as it has a time complexity of O(mn).
Longest Consecutive Sequence
Given an unsorted array of integers nums, return the length of the longest consecutive elements sequence.
You must write an algorithm that runs in O(n) time.
Example 1:
1Input: nums = [100,4,200,1,3,2]
2Output: 4
3Explanation: The longest consecutive elements sequence is [1, 2, 3, 4]. Therefore its length is 4.
Example 2:
1Input: nums = [0,3,7,2,5,8,4,6,0,1]
2Output: 9
1class Solution:
2 def longestConsecutive(self, nums: List[int]) -> int:
3 # Create a set to store the elements in the array
4 num_set = set(nums)
5 longest_seq = 0
6
7 # Iterate through the array
8 for num in nums:
9 # Check if this element is the start of a consecutive sequence
10 if num - 1 not in num_set:
11 # Find the length of the consecutive sequence starting from this element
12 cur_seq = 1
13 while num + cur_seq in num_set:
14 cur_seq += 1
15 # Update the longest consecutive sequence length if necessary
16 longest_seq = max(longest_seq, cur_seq)
17
18 return longest_seq
This algorithm has a time complexity of O(n), since we only iterate through the array once and all other operations (adding to a set and checking if an element is in a set) have a time complexity of O(1).
Maximum Depth of Binary Tree
Given the root of a binary tree, return its maximum depth.
A binary tree's maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.
Example 1:
1Input: root = [3,9,20,null,null,15,7]
2Output: 3
Example 2:
1Input: root = [1,null,2]
2Output: 2
1# Definition for a binary tree node.
2class TreeNode:
3 def __init__(self, val=0, left=None, right=None):
4 self.val = val
5 self.left = left
6 self.right = right
7
8class Solution:
9 def maxDepth(self, root: Optional[TreeNode]) -> int:
10 # Base case: if the root is None, return 0
11 if not root:
12 return 0
13
14 # Recursively find the maximum depth of the left and right subtrees
15 left_depth = self.maxDepth(root.left)
16 right_depth = self.maxDepth(root.right)
17
18 # Return the maximum depth of the left and right subtrees, plus 1 for the root node
19 return max(left_depth, right_depth) + 1
The time complexity of the above code is O(n), where n is the number of nodes in the binary tree. This is because the function is called once for each node in the tree, and the work done in each call is constant (O(1)).
The space complexity is also O(n), since the maximum size of the call stack will be n when the tree is a degenerate tree (i.e., a tree that is a linked list). This is because at each level of the tree, we need to store a function call on the call stack. In the worst case, the tree is a linked list, so we will have n function calls on the call stack.
Same Tree
Given the roots of two binary trees p and q, write a function to check if they are the same or not.
Two binary trees are considered the same if they are structurally identical, and the nodes have the same value.
Example 1:

1Input: p = [1,2,3], q = [1,2,3]
2Output: true
Example 2:

1Input: p = [1,2], q = [1,null,2]
2Output: false
1# Definition for a binary tree node.
2class TreeNode:
3 def __init__(self, val=0, left=None, right=None):
4 self.val = val
5 self.left = left
6 self.right = right
7
8class Solution:
9 def isSameTree(self, p: Optional[TreeNode], q: Optional[TreeNode]) -> bool:
10 # If both nodes are None, return True
11 if not p and not q:
12 return True
13
14 # If one of the nodes is None but the other is not, return False
15 if not p or not q:
16 return False
17
18 # If the values of the nodes are not equal, return False
19 if p.val != q.val:
20 return False
21
22 # Recursively check if the left and right subtrees are the same
23 return (
24 self.isSameTree(p.left, q.left) and
25 self.isSameTree(p.right, q.right)
26 )
The time complexity of the above code is O(n), where n is the number of nodes in the binary tree. This is because the function is called once for each node in the tree, and the work done in each call is constant (O(1)).
The space complexity is also O(n), since the maximum size of the call stack will be n when the tree is a degenerate tree (i.e., a tree that is a linked list). This is because at each level of the tree, we need to store a function call on the call stack. In the worst case, the tree is a linked list, so we will have n function calls on the call stack.
Invert Binary Tree
Given the root of a binary tree, invert the tree, and return its root.
1Input: root = [4,2,7,1,3,6,9]
2Output: [4,7,2,9,6,3,1]
1# Definition for a binary tree node.
2# class TreeNode:
3# def __init__(self, val=0, left=None, right=None):
4# self.val = val
5# self.left = left
6# self.right = right
7
8
9class Solution:
10 def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
11
12 if root:
13 root.left, root.right = self.invertTree(root.right), self.invertTree(root.left)
14
15 return root
The time complexity of the above code is O(n), where n is the number of nodes in the binary tree. This is because the invertTree function is called once for each node in the tree, and the work done in each call is constant (O(1)).
The space complexity is also O(n), since the maximum size of the call stack will be n when the tree is a degenerate tree (i.e., a tree that is a linked list). This is because at each level of the tree, we need to store a function call on the call stack. In the worst case, the tree is a linked list, so we will have n function calls on the call stack.
Binary Tree Level Order Traversal
Given the root of a binary tree, return the level order traversal of its nodes' values. (i.e., from left to right, level by level).
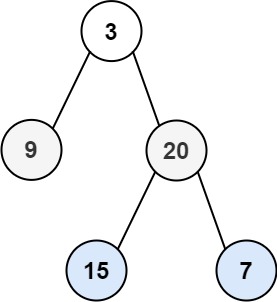
1Input: root = [3,9,20,null,null,15,7]
2Output: [[3],[9,20],[15,7]]
1# Definition for a binary tree node.
2class TreeNode:
3 def __init__(self, val=0, left=None, right=None):
4 self.val = val
5 self.left = left
6 self.right = right
7
8# This code performs a breadth-first traversal of a binary tree and returns a list of lists,
9# where each inner list represents the values at a particular level of the tree.
10
11
12class Solution:
13 def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
14 # Initialize an empty queue and two empty lists to store the result and the current level
15 queue = []
16 result = []
17 level = []
18
19 # If the root node is not None, add it to the queue
20 if root:
21 queue.append(root)
22
23 # While the queue is not empty
24 while queue:
25 # For each node in the queue (i.e., for each node in the current level)
26 for _ in range(len(queue)):
27 # Remove the first node from the queue and add its value to the current level
28 node = queue.pop(0)
29 level.append(node.val)
30
31 # If the node has a left child, add it to the queue
32 if node.left:
33 queue.append(node.left)
34
35 # If the node has a right child, add it to the queue
36 if node.right:
37 queue.append(node.right)
38
39 # Add the current level to the result
40 result.append(level)
41
42 # Reset the current level
43 level = []
44
45 # Return the result
46 return result
The time complexity of this code is O(n), where n is the number of nodes in the binary tree. This is because the function is called once for each node in the tree, and the work done in each call is constant (O(1)).
The space complexity is also O(n), since the maximum size of the call stack will be n when the tree is a degenerate tree (i.e., a tree that is a linked list). This is because at each level of the tree, we need to store a function call on the call stack.
Binary Tree Maximum Path Sum
Given the root of a binary tree, return the maximum path sum of any non-empty path.
Example 1:

1Input: root = [1,2,3]
2Output: 6
3Explanation: The optimal path is 2 -> 1 -> 3 with a path sum of 2 + 1 + 3 = 6.
Example 2:
1Input: root = [-10,9,20,null,null,15,7]
2Output: 42
3Explanation: The optimal path is 15 -> 20 -> 7 with a path sum of 15 + 20 + 7 = 42.
1# Definition for a binary tree node.
2class TreeNode:
3 def __init__(self, val=0, left=None, right=None):
4 self.val = val
5 self.left = left
6 self.right = right
7
8
9class Solution:
10 def maxPathSum(self, root: TreeNode) -> int:
11 # Initialize the maximum path sum to the minimum possible value
12 max_sum = float('-inf')
13
14 def helper(node):
15 nonlocal max_sum
16
17 # If the node is None, return 0
18 if not node:
19 return 0
20
21 # Recursively find the maximum path sum of the left and right subtrees
22 left_sum = helper(node.left)
23 right_sum = helper(node.right)
24
25 # Update the maximum path sum with the current node
26 # and the maximum path sum of the left and right subtrees
27 max_sum = max(max_sum, node.val + left_sum + right_sum)
28
29 # Return the maximum path sum that includes the current node
30 # and either the left or right subtree
31 return max(node.val + left_sum, node.val + right_sum, 0)
32
33 # Find the maximum path sum using the helper function
34 helper(root)
35
36 # Return the maximum path sum
37 return max_sum
38
39
40if __name__ == '__main__':
41 # Test the solution
42 root = TreeNode(1)
43 root.left = TreeNode(2)
44 root.right = TreeNode(3)
45 print(Solution().maxPathSum(root)) # Output: 6
Time & Space complexity:
$$ O(n) $$
Subtree of Another Tree
Given the roots of two binary trees root and subRoot, return true if there is a subtree of root with the same structure and node values of subRoot and false otherwise.
A subtree of a binary tree tree is a tree that consists of a node in tree and all of this node's descendants. The tree tree could also be considered as a subtree of itself.
Example 1:

1Input: root = [3,4,5,1,2], subRoot = [4,1,2]
2Output: true
Example 2:
1Input: root = [3,4,5,1,2,null,null,null,null,0], subRoot = [4,1,2]
2Output: false
1# Definition for a binary tree node.
2class TreeNode:
3 def __init__(self, val=0, left=None, right=None):
4 self.val = val
5 self.left = left
6 self.right = right
7
8
9class Solution:
10 def isSubtree(self, root: Optional[TreeNode], subRoot: Optional[TreeNode]) -> bool:
11 # if the subRoot is empty, then it is a subtree of root
12 # return True
13 if subRoot is None:
14 return True
15
16 if root is None:
17 return False
18
19 # if the root and subRoot are the same tree, then return True
20 if self.isSameTree(root, subRoot):
21 return True
22
23 # if the root and subRoot are not the same tree, then check the left and right subtree
24 return self.isSubtree(root.left, subRoot) or self.isSubtree(root.right, subRoot)
25
26
27 def isSameTree(self, p, q):
28 if p is None and q is None:
29 return True
30 if p is None or q is None:
31 return False
32 if p.val != q.val:
33 return False
34 # when same tree, return True, else return False
35 return self.isSameTree(p.left, q.left) and self.isSameTree(p.right, q.right)
The time complexity of the isSubtree function is O(n^2) in the worst case, where n is the number of nodes in the root tree. This is because in the worst case, the function will need to traverse the entire root tree and for each node, it will also need to traverse the entire subRoot tree to check if they are the same tree.
The space complexity of the isSubtree function is O(n) in the worst case, where n is the number of nodes in the root tree. This is because in the worst case, the function will need to store all the nodes in the root tree in the call stack during the recursive calls.
The time complexity of the isSameTree function is O(n), where n is the number of nodes in the p tree. This is because in the worst case, the function will need to traverse the entire p tree to check if it is the same as the q tree.
The space complexity of the isSameTree function is O(n) in the worst case, where n is the number of nodes in the p tree. This is because in the worst case, the function will need to store all the nodes in the p tree in the call stack during the recursive calls.
Construct Binary Tree from Preorder and Inorder Traversal
Given two integer arrays preorder and inorder where preorder is the preorder traversal of a binary tree and inorder is the inorder traversal of the same tree, construct and return the binary tree.
1Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
2Output: [3,9,20,null,null,15,7]
1# Definition for a binary tree node.
2 class TreeNode:
3 def __init__(self, val=0, left=None, right=None):
4 self.val = val
5 self.left = left
6 self.right = right
7
8
9class Solution:
10 def buildTree(self, preorder: List[int], inorder: List[int]) -> Optional[TreeNode]:
11 # if either preorder or inorder is empty, return None
12 if not preorder or not inorder:
13 return None
14
15 # get the root node from the preorder list and find its index in the inorder list
16 root_val = preorder.pop(0)
17 root_index = inorder.index(root_val)
18
19 # create the root node using the value from the inorder list
20 root = TreeNode(inorder[root_index])
21
22 # recursively build the left and right subtrees using the elements before and after the root node in the inorder list
23 root.left = self.buildTree(preorder, inorder[0: root_index])
24 root.right = self.buildTree(preorder, inorder[root_index + 1: ])
25
26 return root
The time complexity of the buildTree function is O(n^2) in the worst case, where n is the number of nodes in the binary tree. This is because in the worst case, the function will need to traverse the entire preorder and inorder lists for each recursive call.
The space complexity of the buildTree function is O(n) in the worst case, where n is the number of nodes in the binary tree. This is because in the worst case, the function will need to store all the nodes in the binary tree in the call stack during the recursive calls.
Validate Binary Search Tree
Given the root of a binary tree, determine if it is a valid binary search tree (BST).
A valid BST is defined as follows:
- The left subtree of a node contains only nodes with keys less than the node's key.
- The right subtree of a node contains only nodes with keys greater than the node's key.
- Both the left and right subtrees must also be binary search trees.
Example 1:
1Input: root = [2,1,3]
2Output: true
Example 2:
1Input: root = [5,1,4,null,null,3,6]
2Output: false
3Explanation: The root node's value is 5 but its right child's value is 4.
1# Definition for a binary tree node.
2class TreeNode:
3 def __init__(self, val=0, left=None, right=None):
4 self.val = val
5 self.left = left
6 self.right = right
7
8class Solution:
9 def isValidBST(self, root: Optional[TreeNode]) -> bool:
10 """
11 A BST is a binary tree in which the values of the left and right
12 subtrees of every node are strictly less than and greater than,
13 respectively, the value of the node.
14
15 """
16 # get the inorder traversal of the tree
17 output = self.inorder(root)
18
19 # check if the values in the inorder traversal are in ascending order
20 for i in range(1, len(output)):
21 if output[i] <= output[i-1]:
22 return False
23
24 return True
25
26
27 def inorder(self, root):
28 """
29 Get the inorder traversal of a binary tree.
30 """
31 # if the root is None, return an empty list
32 if not root:
33 return []
34
35 # get the inorder traversal of the left subtree, append the root value,
36 # and then append the inorder traversal of the right subtree
37 return self.inorder(root.left) + [root.val] + self.inorder(root.right)
The time complexity of the isValidBST function is O(n), where n is the number of nodes in the binary tree. This is because the function needs to traverse the entire tree to get the inorder traversal and then check if the values in the traversal are in ascending order.
The space complexity of the isValidBST function is O(n) in the worst case, where n is the number of nodes in the binary tree. This is because in the worst case, the function will need to store all the values in the inorder traversal in a list.
The time complexity of the inorder function is O(n), where n is the number of nodes in the binary tree. This is because the function needs to traverse the entire tree to get the inorder traversal.
The space complexity of the inorder function is O(n) in the worst case, where n is the number of nodes in the binary tree. This is because in the worst case, the function will need to store all the nodes in the binary tree in the call stack during the recursive calls.
Kth Smallest Element in a BST
Given the root of a binary search tree, and an integer k, return the kth smallest value (1-indexed) of all the values of the nodes in the tree.
Example 1:

1Input: root = [3,1,4,null,2], k = 1
2Output: 1
Example 2:
1Input: root = [5,3,6,2,4,null,null,1], k = 3
2Output: 3
1# Definition for a binary tree node.
2class TreeNode:
3 def __init__(self, val=0, left=None, right=None):
4 self.val = val
5 self.left = left
6 self.right = right
7
8class Solution:
9 def kthSmallest(self, root: Optional[TreeNode], k: int) -> int:
10 # get the inorder traversal of the BST
11 output = self.inorder(root)
12
13 # sort the list in ascending order
14 output.sort()
15
16 # return the kth element from the sorted list
17 return output[k-1] # -1 because it's 1 indexed
18
19
20 def inorder(self, root):
21 """
22 Get the inorder traversal of a binary tree.
23 """
24 # if the root is None, return an empty list
25 if not root:
26 return []
27
28 # get the inorder traversal of the left subtree, append the root value,
29 # and then append the inorder traversal of the right subtree
30 return self.inorder(root.left) + [root.val] + self.inorder(root.right)
The time complexity of the kthSmallest function is O(n log n), where n is the number of nodes in the BST. This is because the function needs to traverse the entire BST to get the inorder traversal and then sort the list in ascending order.
The space complexity of the kthSmallest function is O(n) in the worst case, where n is the number of nodes in the BST. This is because in the worst case, the function will need to store all the values in the inorder traversal in a list.
The time complexity of the inorder function is O(n), where n is the number of nodes in the binary tree. This is because the function needs to traverse the entire tree to get the inorder traversal.
The space complexity of the inorder function is O(n) in the worst case, where n is the number of nodes in the binary tree. This is because in the worst case, the function will need to store all the nodes in the binary tree in the call stack during the recursive calls.
Lowest Common Ancestor of a Binary Search Tree
Given a binary search tree (BST), find the lowest common ancestor (LCA) node of two given nodes in the BST.
According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”
Example 1:
1Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
2Output: 6
3Explanation: The LCA of nodes 2 and 8 is 6.
Example 2:

1Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
2Output: 2
3Explanation: The LCA of nodes 2 and 4 is 2, since a node can be a descendant of itself according to the LCA definition.
1# Definition for a binary tree node.
2class TreeNode:
3 def __init__(self, x):
4 self.val = x
5 self.left = None
6 self.right = None
7
8class Solution:
9 def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
10 # if p and q are both smaller than root, they are in the left subtree
11 if p.val < root.val and q.val < root.val:
12 return self.lowestCommonAncestor(root.left, p, q)
13
14 # if p and q are both greater than root, they are in the right subtree
15 if p.val > root.val and q.val > root.val:
16 return self.lowestCommonAncestor(root.right, p, q)
17
18 # otherwise, they are on different sides (or equal) and the root is LCA
19 return root
Implement Trie (Prefix Tree)
A trie (pronounced as "try") or prefix tree is a tree data structure used to efficiently store and retrieve keys in a dataset of strings. There are various applications of this data structure, such as autocomplete and spellchecker.
Implement the Trie class:
Trie()Initializes the trie object.void insert(String word)Inserts the stringwordinto the trie.boolean search(String word)Returnstrueif the stringwordis in the trie (i.e., was inserted before), andfalseotherwise.boolean startsWith(String prefix)Returnstrueif there is a previously inserted stringwordthat has the prefixprefix, andfalseotherwise.
1Input
2["Trie", "insert", "search", "search", "startsWith", "insert", "search"]
3[[], ["apple"], ["apple"], ["app"], ["app"], ["app"], ["app"]]
4Output
5[null, null, true, false, true, null, true]
6
7Explanation
8Trie trie = new Trie();
9trie.insert("apple");
10trie.search("apple"); // return True
11trie.search("app"); // return False
12trie.startsWith("app"); // return True
13trie.insert("app");
14trie.search("app"); // return True
1class Trie:
2 def __init__(self):
3 # Initialize an empty dictionary as the root of the Trie
4 self.root = {}
5
6 def insert(self, word: str) -> None:
7 # Start at the root node
8 node = self.root
9
10 # Iterate through each character in the word
11 for c in word:
12 # If the character is not already a key in the current node,
13 # add it as a key and set its value to an empty dictionary
14 node = node.setdefault(c, {})
15
16 # Add the special character '#' to mark the end of the word
17 node['#'] = '#'
18
19 def search(self, word: str) -> bool:
20 # Start at the root node
21 node = self.root
22
23 # Iterate through each character in the word
24 for c in word:
25 # If the character is not a key in the current node,
26 # return False as the word is not present in the Trie
27 if c not in node:
28 return False
29 # Otherwise, move to the next node in the Trie
30 node = node[c]
31
32 # Return True if the special character '#' is present in the current node,
33 # indicating that the word is present in the Trie
34 return '#' in node
35
36
37 def startsWith(self, prefix: str) -> bool:
38 # Start at the root node
39 node = self.root
40
41 # Iterate through each character in the prefix
42 for c in prefix:
43 # If the character is not a key in the current node,
44 # return False as the prefix is not present in the Trie
45 if c not in node:
46 return False
47 # Otherwise, move to the next node in the Trie
48 node = node[c]
49
50 # Return True as the prefix is present in the Trie
51 return True
Author: Sadman Kabir Soumik